Es ist ein alter Hut und wurde vielleicht auch schon bei Euch im Matheunterricht durchexerziert:
Der Umfang der Erde am Äquator beträgt 40.074,9984km (Quelle: Wikipedia, Stand: März 2008). Sagen wir der Einfachheit halber, es seien genau 40.000km und der Äquator wäre ein perfekter Kreis.
Um den Äquator wird nun ein Seil von 40.000 km + 1 Meter gelegt, also ein Seil daß etwas länger als der Äquator ist.
Dieser eine Meter verteilt sich schön gleichmäßig über die gesamte Länge des Äquators, sodaß das Seil überall etwas vom Boden weg ist.
Nun kann man zwei Dinge ausrechnen. Zum einen: Wieviel Millimeter, Zentimeter oder gar Meter steht das Seil vom Boden ab?
Und zum anderen: Wenn es jetzt nicht überall gleichmäßig absteht, sondern man es so hoch vom Boden wegzieht, wie es geht, es also überall sonst glatt anliegt, wie weit könnte man es heben?
Ja und man könnte noch ausrechnen, wie weit die beiden Punkte voneinander entfernt sind, wo es sich dann von der Erdoberfläche ablöst.
Kann man alles ausrechnen, muß man aber nicht, das kann man gerne auch googeln.
Nun lautet meine Frage:
Was paßt im zweiten Fall, also wenn das Seil überall glatt anliegt und nur an einer Stelle so hoch wie möglich angehoben wird, unter dem Seil durch?
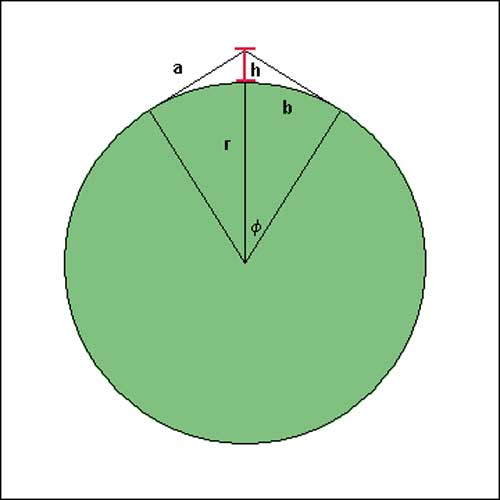
Zur Verdeutlichung habe ich eine Skizze gemalt, gemeint ist Höhe h (rot).
Also, was paßt drunter durch?
a) eine Ameise
b) eine Maus
c) ein Mensch
d) ein Auto
e) ein Bus
f) ein Einfamilienhaus
g) ein Hochhaus mit 12 Stockwerken
h) die St. Barbara-Kirche in Essen-Kray
Ganz ohne Hilfestellung will ich Euch nicht alleine lassen: LINK
Der oder die richtige(n) Lösungsbuchstabe(n) kommen auf Euren Lösungszettel.
Ich habe noch einmal die wichtigsten Schlagwörter (Hashtags) dieses Artikels für Sie zusammengestellt, damit Sie sich besser orientieren können:
Keine Schlagwörter vorhanden
Nur eine kurze Verständnisfrage:
„Der oder die richtige(n) Lösungsbuchstabe(n)“ bedeutet, wenn das Seil 10 Zentimeter absteht, ist die Lösung „ab“, weil sowohl eine Ameise als auch eine Maus drunter durch passt, richtig?
Das Größtmögliche.
Ist doch klar, wenn ein Ozeandampfer drunter durchpaßt, dann passt auch ein Ruderboot und alles was kleiner ist als ein Ozeandampfer drunter durch.
Also nur der(!) Lösungsbuchstabe des größtmöglichen und nicht etwa mehrere Lösungsbuchstaben?
Na für das bisschen Schulmathematik wird man ja wohl nicht googeln müssen 🙂
Wie gut, dass du so klug bist. Ich verneige mein ergrautes Haupt vor dir.
Zählt es, wenn ein Mensch kriechend durchpasst?
Man muß ja nicht kriechen. Man könnte auch Limbo durchtanzen. 🙂
Sofern man druchpaßt nartürlich.
Das Ergebnis wird manche überraschen 🙂